Addition
Wie im vorherigen Artikel Zahlensysteme gesehen, ist die Addition von zwei Binärzahlen sehr einfach.
Es gibt hier für die Ziffer ganz rechts nur 4 Möglichkeiten, die in der folgenden Wahrheitstabelle abgebildet sind:
| A | B | Q | C |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Q ist das Ergebnis der Addition, C ist das Übertrags-Bit oder englisch "carry" Bit.
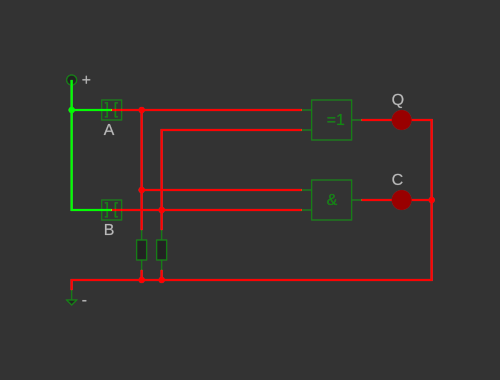
Betrachtet man nur das Q, ist die Tabelle identisch zu einem XOR, betrachtet man nur das C-Bit ist es ein UND.
Also als Logik:
Dies ist ein sogenannter Halb-Addierer.
Für die anderen Bits ist das jedoch noch nicht genug, da wir hier noch das Übertrag Bit des Vorgängers brauchen.
Die Tabelle wird dadurch größer:
|
C (Vorgänger) |
A | B | Q | C |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Für den Fall C=0 gilt, Q=A XOR B,
Sobald C 1 ist, wird Q invertiert, erneut das verflixte XOR:
Q=(A XOR B) XOR C
Für C ist es komplizierter.
Im Fall C(Vorgänger) = 0 verhält es sich wie ein UND,
Im Fall C(Vorgänger) = 1 verhält es sich wie ein A ODER B.
Wenn wir nun A XOR B nehmen (das Zwischenergebnis von oben), das mit C(Vorgänger) verunden, bekommen wir die untere Hälfte der obigen Tabelle bis auf A=1, B=1.
Nehmen wir nun das A UND B (egal was C macht) und verbinden das per ODER mit dem ersten Teil, haben wir die komplette Logik:
Jetzt müssen wir nur noch 1x den Halbaddierer und 7x den Volladdierer zusammenbauen und wir haben unseren 8-Bit Addierer und eine Menge Chips.
Leider gibt es auch noch ein Problem mit "echten" Chips, bis sich die ganzen Carry-Bits von dem niedrigsten Bit bis zum höchsten Bit weitergesprochen haben vergeht eine gewisse Zeit, die linear wächst, je mehr Bits addiert werden. Dadurch wird die Taktrate eines Addierers beschränkt. Dies zu umgehen, bedarf einigen Zusatzaufwand.
Aber zum Glück gibt es den 74xx283: ein 4-Bit-Volladdierer mit Carry-Ein- und -Ausgang und schneller Carry-Verarbeitung. Typicherweise können diese Chips mit 2-stelligen MHz umgehen, weit über unserem Ziel.
Damit müssen wir nur noch die Ein- und Ausgangsleitungen verbinden, sowie den Carry Ausgang des einen Chips in den Eingang des anderen verbinden.
Die genaue Schaltung erfolgt später, nachdem weitere Funktionen beschrieben wurden.
Zunächst aber ein kleiner Exkurs zu den negativen Binärzahlen