Subtraktion
Bisher haben wir die Addition von Binärzahlen und und negative Binärzahlen gehabt.
Wie sich hoffentlich die meisten noch erinnern können, ist eine Subtraktion auch als eine Addition darzustellen, wenn die 2te Zahl negiert wird. Also z.B. 5-3 ist identisch zu 5 + (-3).
Wenn wir nun unseren Voll-Addierer nehmen und optional die zweite Zahl über das Zweierkomplement invertieren, kann unsere ALU auch subtrahieren.
Nur wie macht man das ohne großen Aufwand:
Fangen wir mit dem optionalen Invertieren an. Hier kommt wieder das XOR ins Spiel. Damit lässt sich ja ein Bit optional invertieren. Zur Erinnerung:
| A | B | Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Wenn wir nun unser Addition bzw. Subtraktionsflag für A nehmen, haben wir einen optionalen Inverter.
Fehlt nun noch das +1. Das ist auch kein Problem, wenn wir für unseren Addierer alle 8 Bits über einen Voll-Addierer lösen, können wir das Signal als Carry-Eingang nehmen. Damit lässt sich das + 1 lösen.
Also addiert unsere ALU, wenn das indikator-Bit eine 0 ist und subtrahiert, wenn es 1 ist.
Zum bauen benötigen wir also 2x den 74xx283 Voll-Addierer und 8x XOR, d.h. 2x den 74xx86.
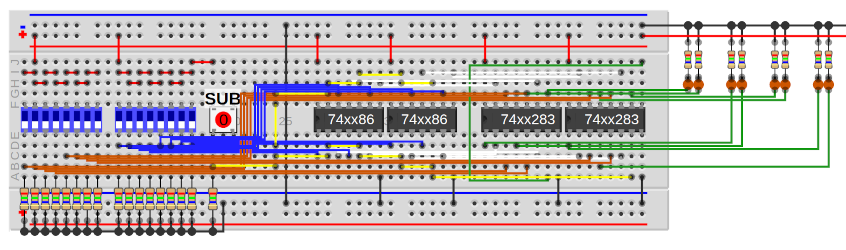
Zusammen ergibt das:
Hier werden folgende Farben verwendet:
- braun für Register 1,
- blau für Register 2,
- gelb für das Substraktions-Flag,
- weiß für die Leitungen von den XORs zu den Addierern,
- grün für die Ausgangs-LEDs
Hier kann man schonmal das addieren und subtrahieren von positiven und negativen Zahlen probieren und üben.
Allerdings gibt es noch 2 Hürden zu nehmen:
- Es müssen noch die echten Register angebunden werden, da gibt es ein paar Fallstricke,
- das Ergebnis muss auch irgendwo speicherbar sein, d.h. in ein Register zurückgeschrieben werden
Die Probleme werden in nächsten Schritt, der Registeradressierung angegangen.